언리얼엔진_UV 커스텀 회전(로테이트) 에 대한 분석 With Dot(내적)

 

일단 언리얼에서 표현하고있는 로테이트 방식을 이해하려면..

우선 미적분과 내적 에 대해 이해를 해야한다

ㅋㅋㅋㅋ...

 

내적 에 대해 정말 디테일하게 알고싶다면

마지막 문서를 확인하면 된다.

 

 

DotProduct

 

우리는 언리얼 방식을 뜯어보기 전에

겸으로 DotProduct 라는 노드에 대해 이해를 해볼것이다.

이를 이해하면 먼저 내적에 대해 이해를 해야한다...

 

하지만! 이번 정리글에선 진짜 깊게깊게 빠지진 않을것이고

최~~~대한 이해하기 쉽게 설명을 할것이다!

 

 

 

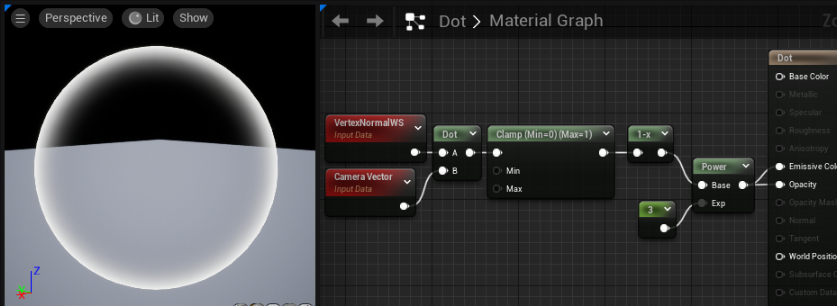
우선 위의 이미지의 원리를 분석해본다면 ( 노드는 무시하고 )

 

가운데 투명한 곳을 보면

우리의 눈의 방향과 가운데에 있는곳이 바라보는 방향이 같기에  투명하게 나오고

 

바깥쪽 색이 나오는 곳을 보면

우리의 눈의 방향과 바깥쪽에 있는곳이 바라보는 방향이 완전히 다르기에 (수직하기에)  점차 불투명하게 나오는 것이다.

 

 

만약 원래대로 VertexNormalWS 와 CameraVector 를 Dot에 연결한다면

정반대의 값이 나올것이다.  이는 저 방어막쉐이더 를 통해 설명하려고 [ 1-x ] 노드를 연결한 것이다.

 

 

 

 

 

정확하게 구하는 값은 다음과 같다.

A벡터가 구체가 바라보는 방향이고

B벡터가 카메라가 바라보는 방향(역방향)이라고 할때

위처럼 되었다고 가정해보자.

 

이때 A와 B의 내적을 구해야하는데

정말정말 쉽게 말하면 A의 종점을  x축에 가까워지도록 아래로 끌어내린값 과 B를 곱한 값 이다.

여기서 B는 1이니 A종점을 끌어내린 |A| Cosθ 크기만 구하면되는데

 

 

여기서 각도에 따라 A의 종점이 달라지는 것을 알 수 있다.

θ의 각도가 작아질수록 값이 커지고

θ의 각도가 커질수록 값이 작이진다.

 

이처럼 DotProduct는

카메라가 바라보는 방향과 일치할수록 1에 가까운 값을 도출해내고

카메라가 바라보는 방향과 수직일수록 0에 가까운 값을 도출해내는 수식인걸 알 수 있다.

 

 

내적의 정확한 계산식은 다음과 같다.

|A| |B| Cosθ

 

 

 

이를 통해 아까보았던 카메라벡터 x 버텍스노말 을 내적해 방어막같은 이펙트를 줄 수도 있다.

 

 

 

 

 

 

Custom Rotator 노드 뜯어보기

 

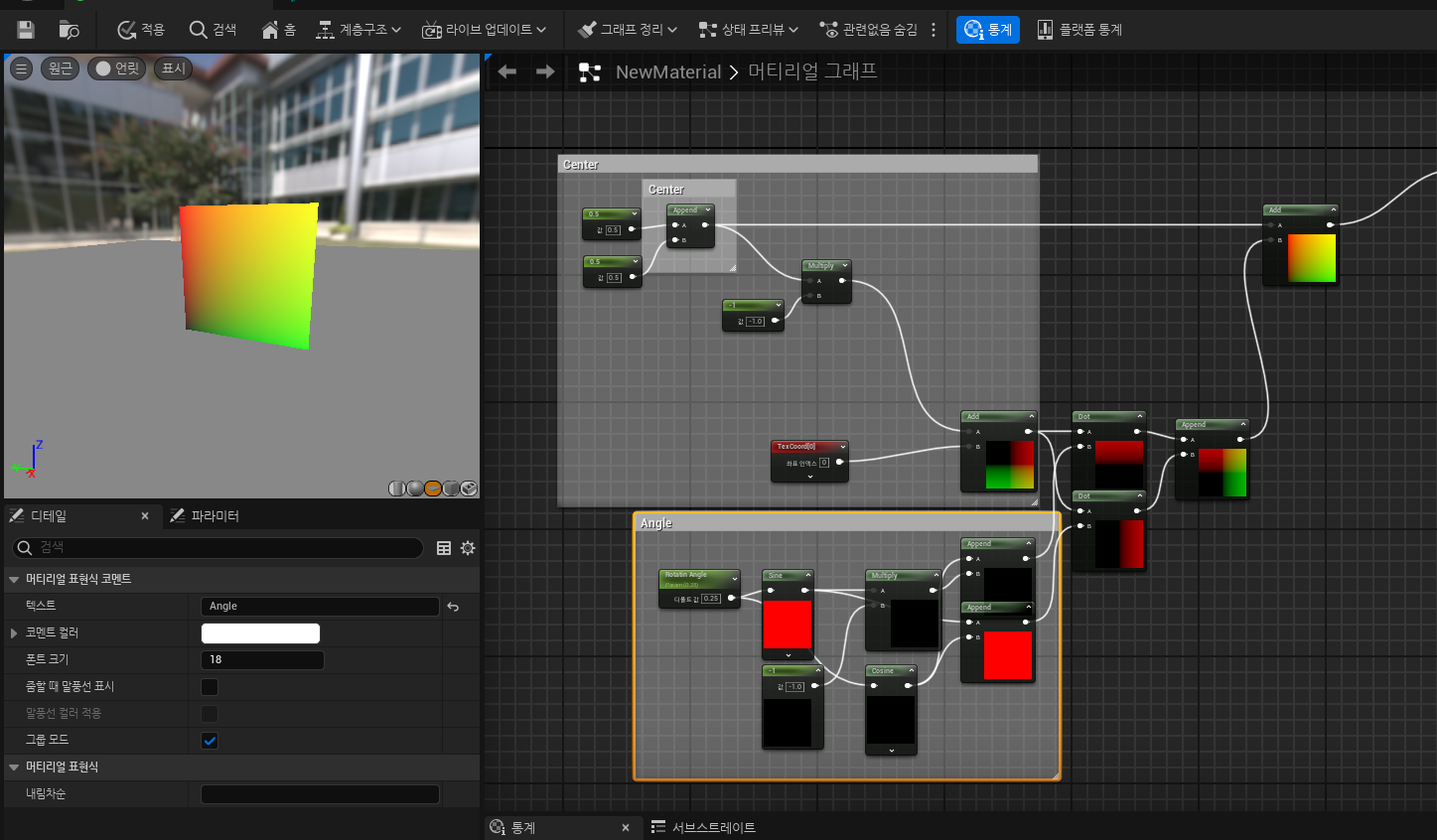
이제 Custom Rorator를 뜯어보자.

구성은 중심점구하기 / UV뒤집기 / 합치기

로 이루어져있다.

 

 

Center 구하기

 

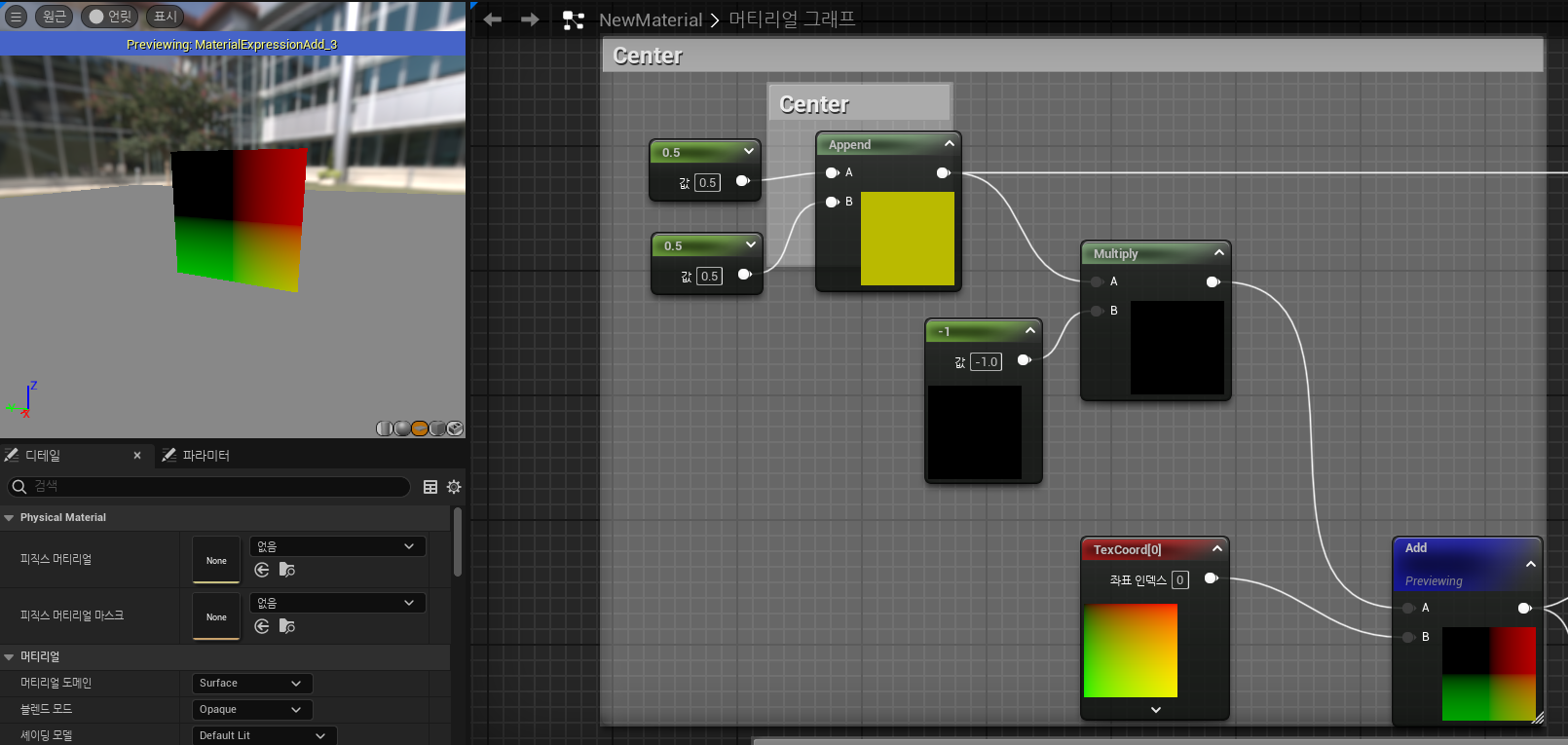
여기서 우리는 중심이 될 곳을 먼저 지정해주는것이다.

만약 정확한 회전을 요구하는것이 아닌

적당한 타일을 사용해서 회전하길 원한다면
스킵해도 좋다.

우린 알고있다시피 좌측상단을 0,0 으로 시작해서

우측하단까지 1,1 흘러간 다는 것을 알 수 있다.

우린 0,0을 기준으로 돌려주는 것이 아닌 중심 0.5기준으로 돌려줄 것이기에

중심점을 먼저 맞춰줘야 한다.

 

 

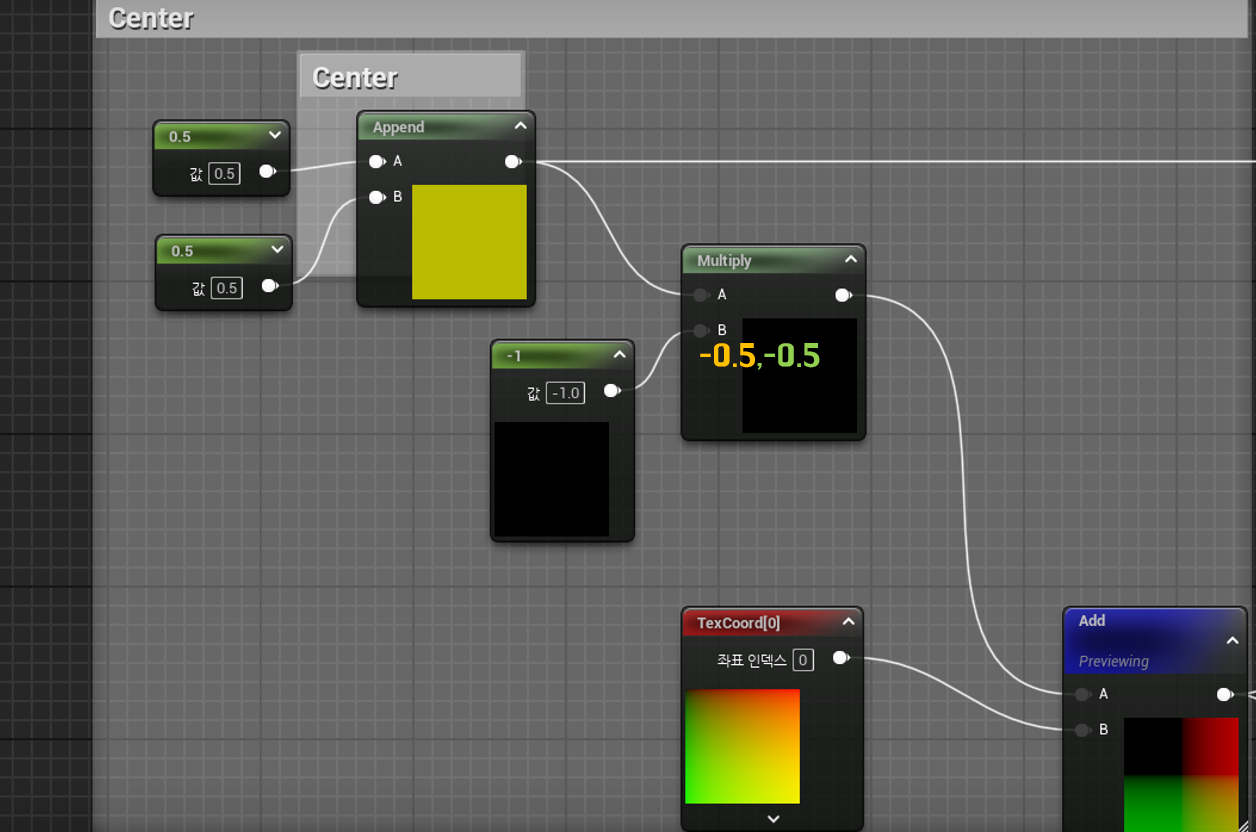
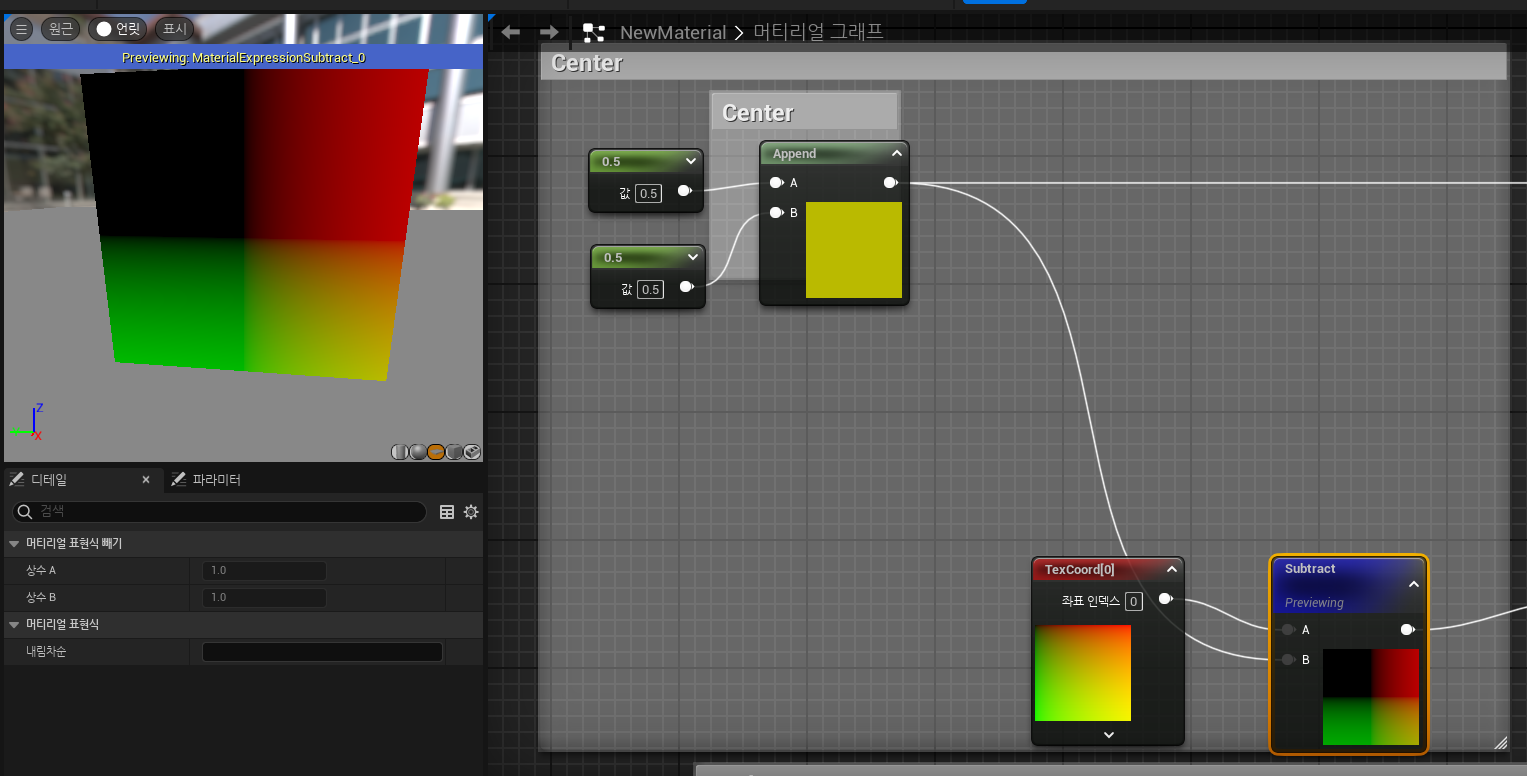
중심점만큼 이동시키기위해

[0.5,0.5]를 바로 빼버리든 , -1을 곱한 뒤 더해버리든

선택하여 다음과 같은 값을 내면 된다.

 

 

Rotator Angle 구현

 

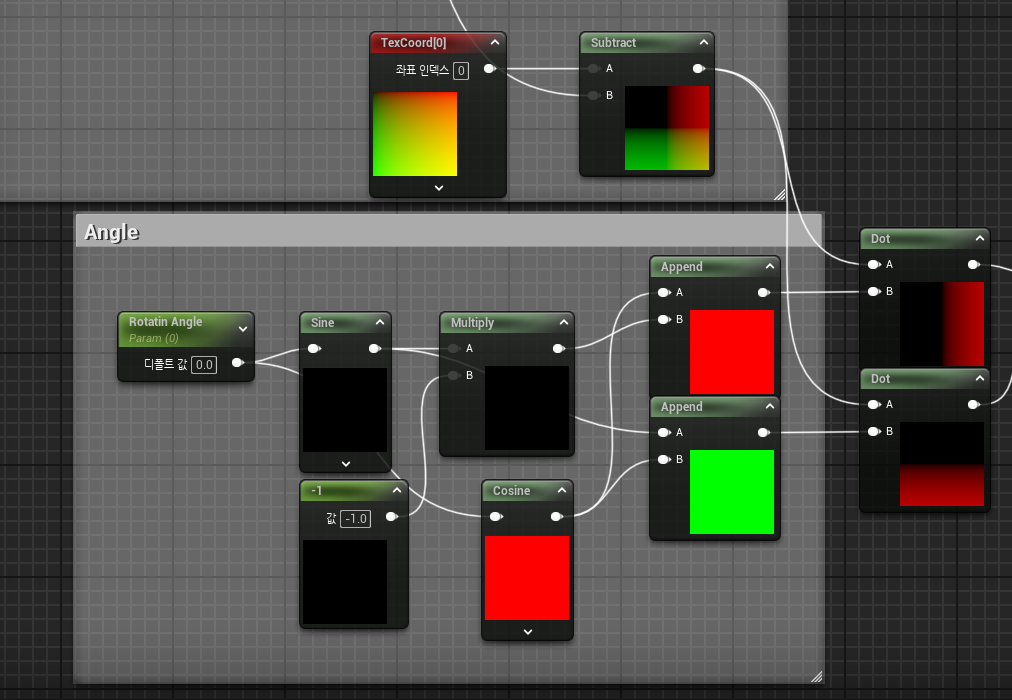
여기서 Rotation Angle값을 0 / 0.25 / 0.5 / 0.75  로 사용할건데

0~1을 넘어갈 때를 대비해 Sine과 Cosine으로 0~1로만 사용되도록 조절한다.

 

 

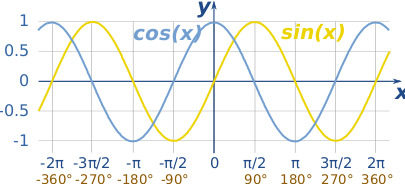
여기서 우리는 Sine과 Cosine에서 각각

0 / 90 / 180 / 270 일때 나오는 값들을 이용해 줄 것이다.

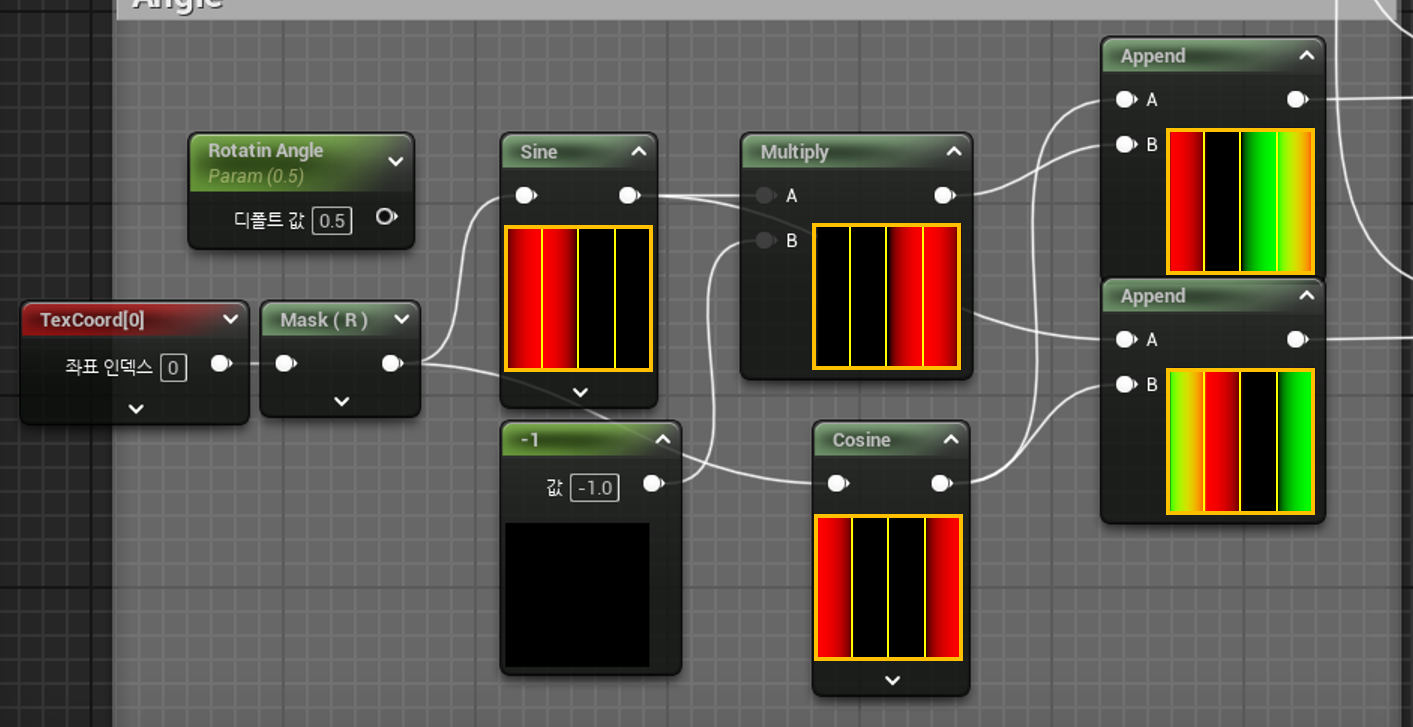
이번엔 각도를 넣는게 아니라

0 ~ 1 로   각각 0 / 90 / 180 / 270 일때 나오는 결과값들을 상자를 통해 구분해줬다.

이를 통해 angle값이 0 / 90 / 180 / 270 일때 나오는 결과를 한눈에 볼 수 잇을것이다.

 

 

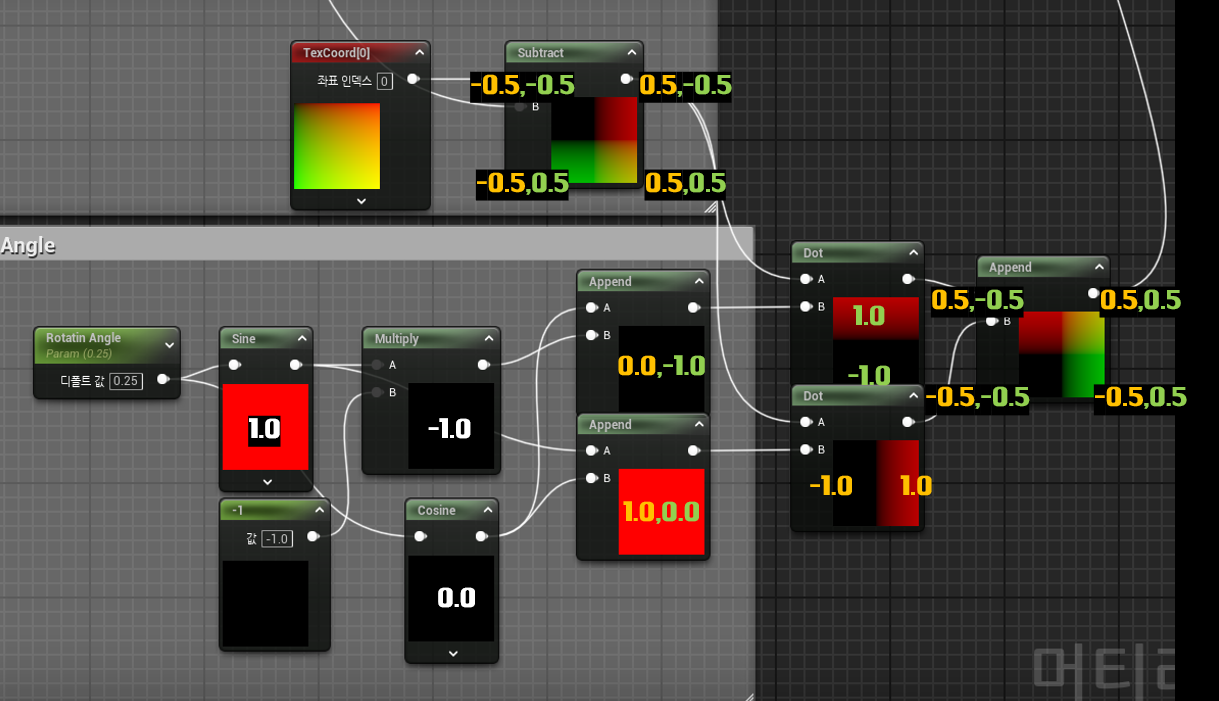
이제 위에서 나온 두 append 값으로

[0.5,0.5] 과의 내적을 구해줄 것이다.

 

이러한 과정을 거치게 된다면 마지막처럼

좌측으로 한번 회전된 UV값을 구할 수 있을것이다.

 

 

합치기

 

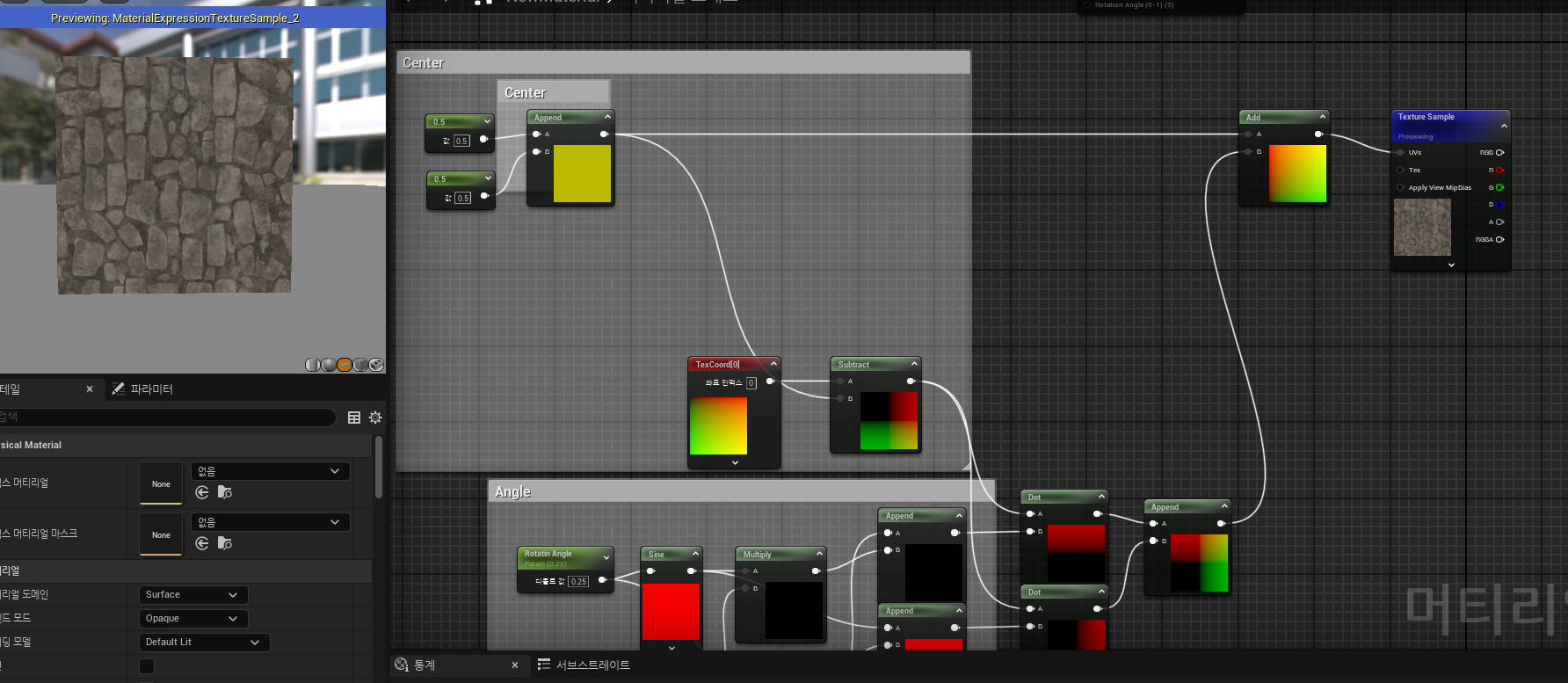
지금구한 좌표값은 피봇이 [0.5,0.5]만큼 빠져있다.

피봇의 위치를 뺴줬다면 다음처럼 합쳐주자.

 

 

 

 

 

 

 

번외1 내가 직접만들어본 Rotator

사실 이번에 이를 분석해 본 이유는

이 단순한 노드에 미적이라던가 기하백터라던가

이렇게 복잡한 노드가 사용된다고??? 하는 의문에서부터 시작되어 뜯어보기 시작했다.

 

추가로 이게 정확히 어떤 역할인지 , 개량화하거나 더 커스텀할 순 없는지가 궁금하여

이렇게 분석하게 되었다.

이제 분석한 토대로 나만의 방식으로 한번 구현해보고 싶었다.

 

 

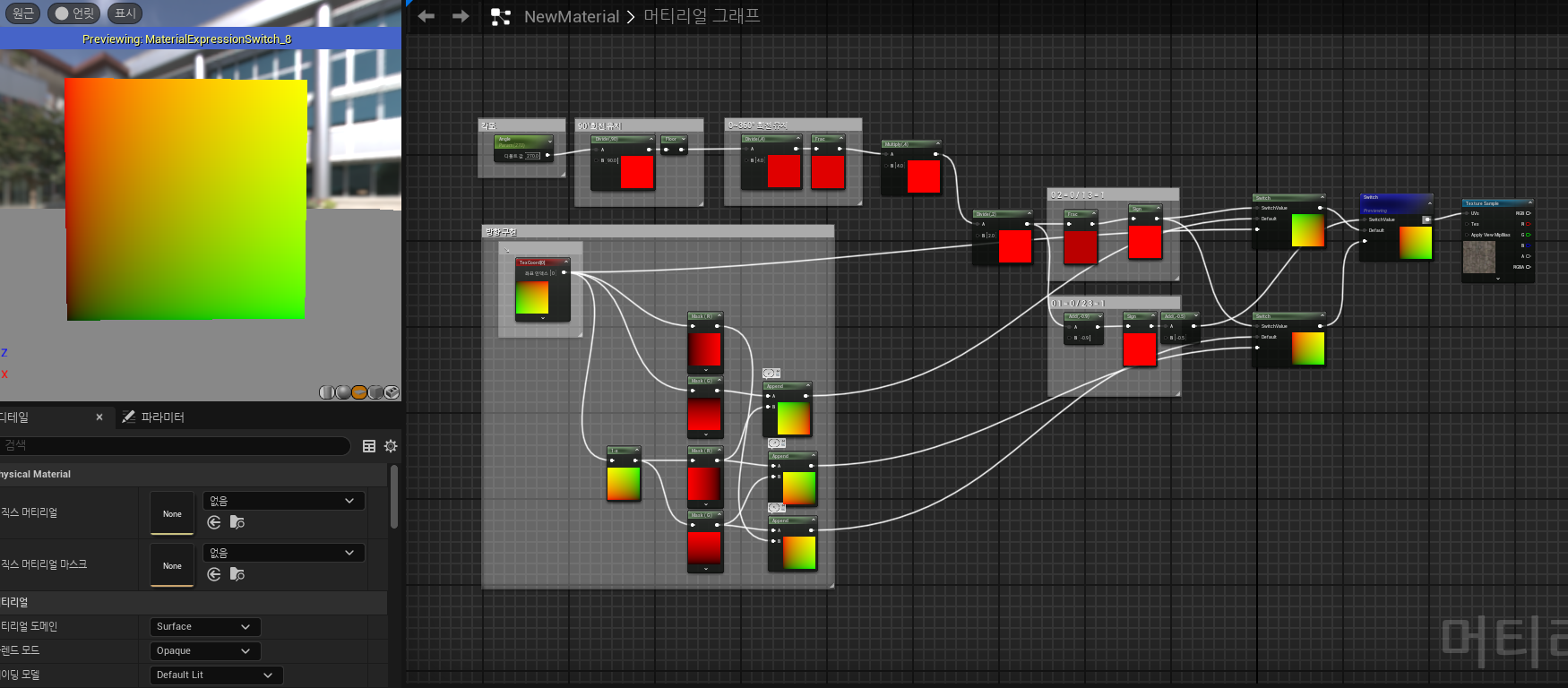
내가 직접 구현한 Rotator 방식은 다음과 같다

ㅋㅋㅋㅋ...

더 복잡해진거같은데...

연산식은 단순해져도 되려 복잡해진거같다

진정 미적이랑 기백이 필요한것인가...

 

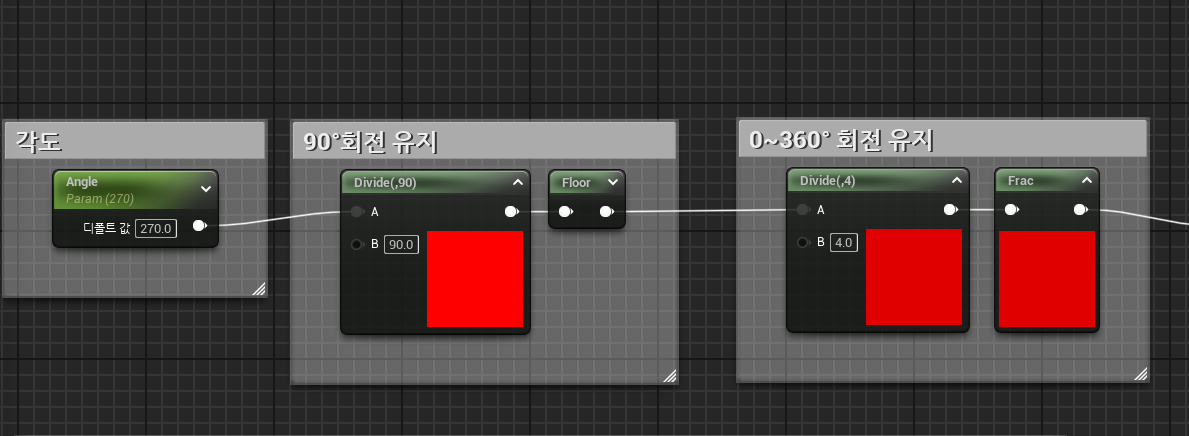
우선적으로 각도조절을 먼저 구현했다.

 

우선적으로 90으로 나누었을때 Floor로 정수 외의 소수점들을 제거해

언제나 90도를 유지하게 되었고

 

4를 나눌때 Frac으로 소수점만 남겨

4 보다 수치가 클때 다시 0으로 초기화 시켜준다.

 

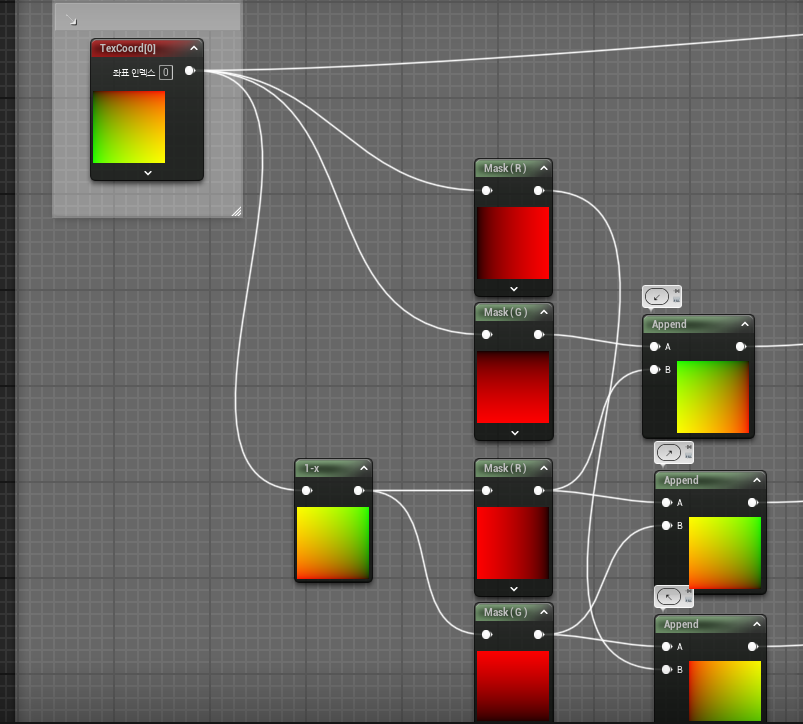
그 다음으론 방향을 구현해주었다.

위의 방식을 사용하지않으니

결국엔 이와같은 노가다가 된게아닌가.. 싶다.

 

 

 

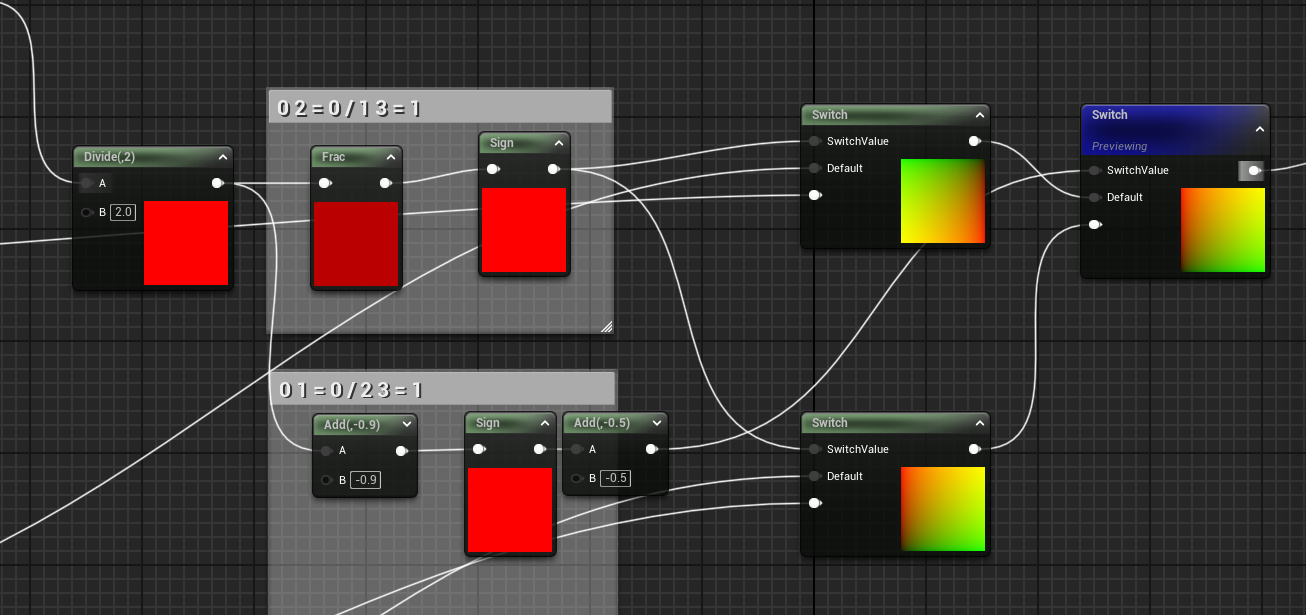
이제 이를 0 , 90 , 180 , 270 일때를 구분할 수 있도록

다음과 같은 방식을 사용해주었다.

 

0    1    2    3  에서 2를 나누어

0  0.5   1   1.5  로 만들어주고

 

Frac을 통해 짝수홀수를 구분해주고

-0.9를 더해 1과 2 경계를 구분해주었다.

 

이를 Switch 에 넣어

0 , 90 , 180 , 270 을 구분해주었다.

 

 

...분명 더 좋은방법이 있겠지만..

혼자서 직접 만들어보는 방식으론 당장은 여기까지인듯하다..

 

그래도 혼자 만들어보면서 새롭게 배운 방식도 있었고

정확히 어떤역할인지 , 무엇이 필요한지를 배울 수 있는 시간이였다.

거.. 배경만들기.. 뭐 쉬운게없네...

 

 

 

 

 

 

https://dev.epicgames.com/documentation/ko-kr/unreal-engine/math-material-expressions-in-unreal-engine?application_version=5.3&utm_source=editor&utm_medium=docs&utm_campaign=rich_tooltips#dotproduct

언리얼 Dot Product에 대한 문서

 

https://dev.epicgames.com/documentation/ko-kr/unreal-engine/math-material-expressions-in-unreal-engine?application_version=5.3&utm_source=editor&utm_medium=docs&utm_campaign=rich_tooltips#sine

언리얼 Sine 에 대한 문서

 

https://wikidocs.net/22384

042. 내적 vs 외적

 

내적에 대한 문서

 

https://jang-inspiration.com/dot-product

Dot Product 정리

Dot Product (내적)

 

https://ballpen.blog/%EB%82%B4%EC%A0%81-%EB%B2%A1%ED%84%B0%EB%81%BC%EB%A6%AC-%EA%B3%B1%ED%95%98%EC%97%AC-%EC%8A%A4%EC%B9%BC%EB%9D%BC%EA%B0%80-%EB%90%98%EB%8A%94-%EA%B3%84%EC%82%B0%EB%B2%95/

내적 - 벡터끼리 곱하여 스칼라가 되는 계산법 - ilovemyage

내적에 대한 추가문서

 

 

 

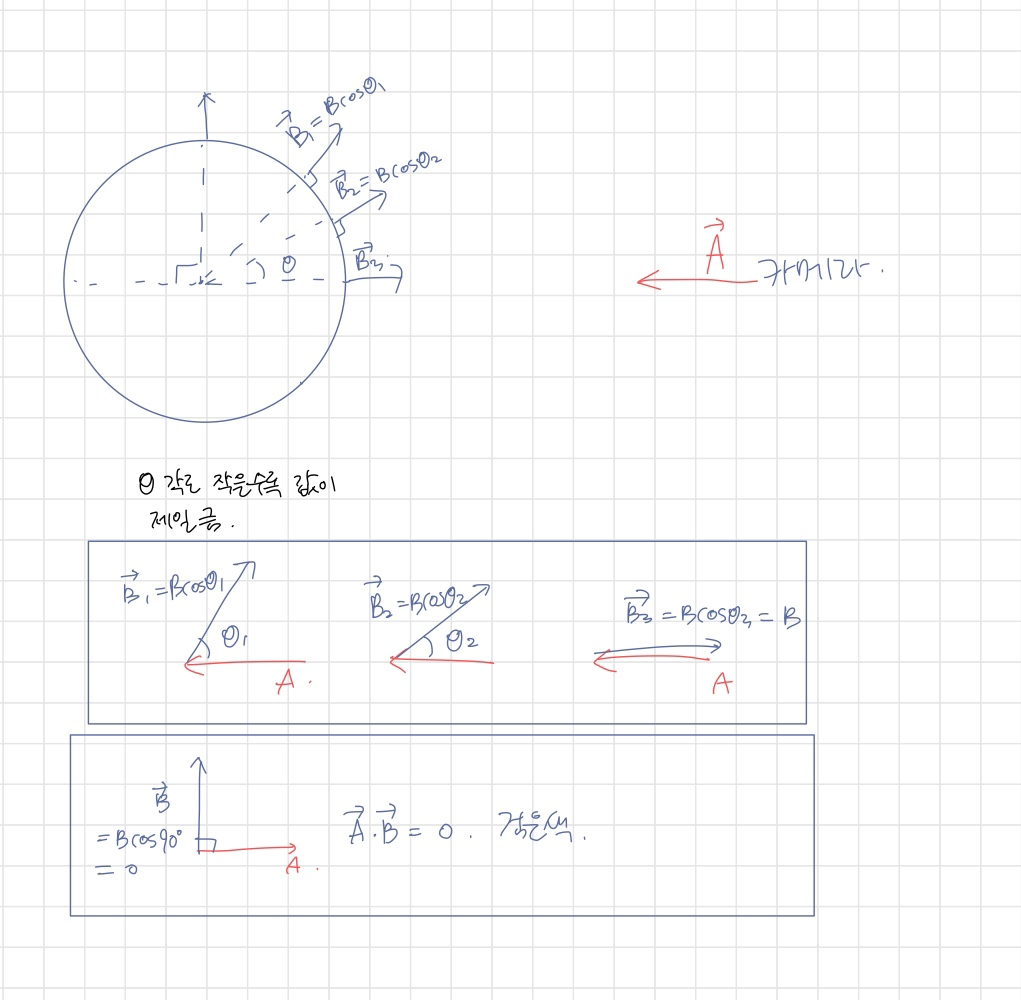
친구가 보내준 이해노트